The State Pattern

State is a behavioral design pattern that modifies an object's behavior based on the current state it is in. This pattern is closely coupled with the Finite-State Machine. Imagine a Door object, which can either be open, closed, or locked. While it is locked, it cannot be open and likewise, while it is open, we cannot lock it, but we can lock it while it is closed. The condition-decision nightmare is obvious even with this simple example.

The primary idea is that there are finite states and at any particular moment, the object can be in one such state. This is used to avoid unnecessary switch-case and if-else conditions in the code, which could be a nightmare to maintain and cause bugs if the number of states is large.

The best approach is to use this pattern wherein implementing the behavior lies with the Object state. A wrapper class is used to delegate the transition calls and return the updated state. This approach can lead to memory leaks if we are creating/destroying states while returning. We can use Singletons to make it leak tolerant and this will work even with multiple Door contexts as the _currState variable holds the current state of that context.

	template <typename T> class DoorCRTP {
	public:
	static T *getInstance() {
	static T* __inst = new T();
	return __inst;
	}
	};

	class OpenState : public DoorState, public DoorCRTP<OpenState> {
	OpenState() = default;
	public:
	friend class DoorCRTP<OpenState>;
	};

	DoorState *OpenState::open() {
	cout << "Door is already open" << endl;
	return OpenState::getInstance();
	}
	DoorState *OpenState::close() {
	cout << "Closing door..." << endl;
	return CloseState::getInstance();
	}
	DoorState *OpenState::ulock() {
	cout << "Door cannot be locked" << endl;
	return OpenState::getInstance();
	}

view raw Door.cpp hosted with ❤ by GitHub

While this approach is the standard GOF implementation, this may not be applicable in every use case. It will only work when we know the state interactions at compile time. Consider the most simple example of RegEx, which has to construct a state machine for one regular expression which represents multiple patterns. There is absolutely no way of knowing or determining the state transitions during runtime and this concrete approach becomes useless. A link to the full source code is here.

State Machines

To implement a basic Finite-State Machine, we need three objects—the State, Trigger, and Transition. There should be some mapping in which we store the desired state for a given transition. In this design, I created the map inside the Trigger object for readability, but there is absolutely no reason why we can't do it on the State object. In the upcoming section where I discuss a problem statement, I've done so in the State object.

Consider the following State diagram. It has 2 States, 2 Triggers, and 4 Transitions. The basic requirement is to create the State machine at runtime. We already made the object classes as seen in the UML, and in this example, I've illustrated how we can use Transitions to get some work done. Ideally, one would want some actions to occur when we transition from state to state or do a default transition. Callbacks are the best ways to implement such a feature. We could've used std::function here, but function pointers do the job equally well in this case.

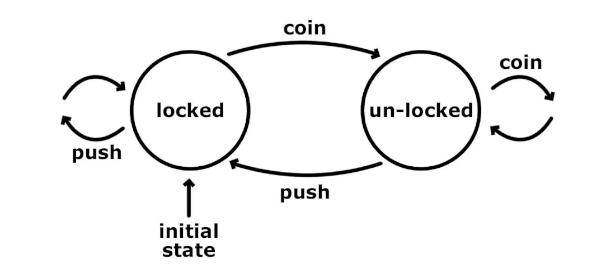
Ideally, we would do the construction by parsing some metadata and maybe use the Interpreter pattern. For simplicity, I directly coded this in the client to make it more readable. You can find the complete example here.

	int main() {

	State* locked = new State;
	State* unlocked = new State;

	Trigger* push = new Trigger;
	Trigger* coin = new Trigger;

	Transition* l2u = new Transition([]() {cout<<"This "<<endl;});
	Transition* u2u = new Transition([]() {cout<<"is "<<endl;});
	Transition* u2l = new Transition([]() {cout<<"the "<<endl;});
	Transition* l2l = new Transition([]() {cout<<"Pattern."<<endl;});

	push->registerTrans(locked, l2l, locked);
	push->registerTrans(unlocked, u2l, locked);
	coin->registerTrans(unlocked, u2u, unlocked);
	coin->registerTrans(locked, l2u, unlocked);

	locked->onTrigger(coin)->onTrigger(coin)->onTrigger(push)->onTrigger(push);

	return 0;
	}

view raw FSM.cpp hosted with ❤ by GitHub

Example Problem

This statement is copied as is from the Udemy course : Design Patterns in Modern C++

State Coding Exercise
A combination lock is a lock that opens after the right digits have been entered. A lock is preprogrammed with a combination 
(e.g., 12345 ) and the user is expected to enter this combination to unlock the lock.
The lock has a status  field that indicates the state of the lock. The rules are:
    If the lock has just been locked (or at startup), the status is LOCKED.
    If a digit has been entered, that digit is shown on the screen. As the user enters more digits, they are added to Status.
    If the user has entered the correct sequence of digits, the lock status changes to OPEN.
    If the user enters an incorrect sequence of digits, the lock status changes to ERROR.
Please implement the CombinationLock class to enable this behavior. Be sure to test both correct and incorrect inputs.

Satisfying the above requirements are easy and we can even do this without using the State pattern. If we add a couple of more constraints like

    If the lock status is OPEN it must remain open unless it was locked with the number of the beast.
    If the lock is in ERROR state, the user is allowed to enter the next inputs seamlessly.

We have bolstered the original problem statement by adding these constraints and now it makes more sense to do it with a custom Pattern matching State machine. Imagine the input sequence be 426789. The corresponding state diagram looks like this. Objects represent the states, and triggers are simple integers. Transitions are implicitly modeled as callbacks inside the LockState object.

I represented two types of states—Valid and Invalid, and there is only one unique sequence for opening the lock. Entering the correct combination sequence will lead to the open state. Entering an incorrect digit(represented by an x) in any state will land you on the invalid trail that will end only in error. Some states have a default transition, like the Open state where the lock remains in that state and I used -1 as the trigger. Used lambdas for callback functions which append the current digit to the Status string and resets upon reaching a terminal state.

Also, I've configured the error state to resume regular operation as one enters new digits. This feature would only be possible if we use state machines in this manner. The structure resembles a Regular Expression representation closely where the state machine progresses based on the input sequence and finds matches in a string. Maybe I overdid this, but I wanted to avoid conditional statements in the states and came up with this structure.

	class LockState {
	string _status;
	map<int, pair<function<string(int, string)>, LockState*>> _trans;

	public:
	LockState* enter_digit(int digit);
	void setTransition(int digit, function<string(int, string)> cb, LockState* state);
	void setStatus(string status);
	string getStatus();
	};

	LockState* LockState::enter_digit(int digit)
	{
	auto it = _trans.find(digit);
	if (it != _trans.end()) {
	auto _tpair = it->second;
	auto newStatus = _tpair.first(digit, _status);
	_tpair.second->setStatus(newStatus);
	return _tpair.second;
	} else {
	auto it = _trans.find(-1);
	auto _tpair = it->second;
	auto newStatus = _tpair.first(digit, _status);
	_tpair.second->setStatus(newStatus);
	return _tpair.second;
	}
	}

view raw PatternMatching.cpp hosted with ❤ by GitHub

Adding more gists here will add more confusion. Click the link for the complete source code. I've used Iterators to set the transitions and callbacks because if we use the array size, then there are plenty of corner cases that show up. With iterators, handling the invariants become easier. We only need to address one corner case in which the length of the combination is just one.